I would like to tell you about one of the oldest branches of mathematics, the geometry.

Geometry is a branch of mathematics, which deals with spatial relations and shapes, and relations and shapes, which have structure such as spatial ones.

The term "geometry" is translated as "measuring of earth".

Geometry in its development passed through four stages. The first one was a period of arising geometry as mathematical science, which was being in Ancient Egypt, Greece and Babylonia before the 5^th century BC. First geometrical knowledge was got, but without proofs. Sometimes this knowledge was false. For example, Egyptians used formula S=ab/2 for square of triangle, but it is true only for right triangle. But ancient mathematicians knew many true theorems. For example, the famous Pythagorean theorem 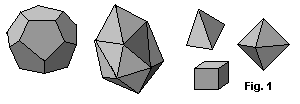used by them too. Another beautiful discovery of that time was five Platon's solids. Ancient mathematician Platon found all regular polyhedrons: the tetrahedron, the hexahedron (or cubes), the dodecahedron and the icosahedron. Only five regular polyhedrons exist, but this fact was proved by Leonard Euler in 18^th century (see fig.1). In the second stage the proofs were entered in geometry by famous mathematician Thales (Фалес). Encyclopedia of the geometrical knowledge of that time was "Beginning"(Начала) by Euclid. It was written about three hundred years BC. The third stage was arising of projective geometry. The outstanding artist and mathematician Albrecht Dürer (Альбрехт Дюрер) investigated the lows of perspective in the 15^th century. But he was not first mathematician, who did it. Before him were Greek mathematician Papp (Папп) and French mathematician Desarg (Дезарг). But Albrecht Dürer was the first man who applied projective geometry and perspective theory in his pictures. He also very likes to draw mathematical objects in his works. One of such pictures is all known "Melancholia". The fourth stage was a period of arising analytical geometry: the part of geometry, where geometrical problems solved using algebraic methods. In the 17^th century Descartes created coordinate method - the main tool of analytical geometry. Nowadays geometry passes the fifth stage, began by Lobachevski in 19^th century. He invented alternative geometry. Lobavhevski's geometry based on the statement that for any line more than one parallel line containing the given point exists. Later Riman generalized this idea and described the variety of geometries. The significance of non-Euclidean geometry was realized earlier in 20^th century, when the goemetry was applied in mathematical physics. It has come to play an essential role in the theory of relativity. In the end of the 19^th century the topology, the new branch of mathematics, devised from geometry. 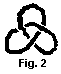Topology is the science about topological invariants, i.e. about properties of a surface non-changing by small deformations. 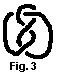First topological theorems were proved by Euler (Эйлер) in the 18^th century: the polyhedral theorem and the theorem about Künigsbergian bridges. But as a new theory topology formed in Poincarè's works. One of the fields in topology is knot theory. It is very beautiful and interesting branch of mathematics, which studied knots and their interlacements. Most famous knots are the shamrock and the eight. (See fig. 2 & fig. 3).

Geometry is the science, in which many usual objects become wonderful and mysterious. Their simple properties seem us increasingly interesting.

Geometry in its development uses methods of all branches of mathematics. It is no mere chance, that the word "geometry" in French language means mathematics as a whole.