

ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ИВТ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
по курсу "Алгоритмические языки и программирование"
тема: "ВРАЩЕНИЕ ОБЪЕМНЫХ ОБЪЕКТОВ ВОКРУГ ПРОИЗВОЛЬНОЙ ОСИ"
ВЫПОЛНИЛ студент гр. В-128
_______________Борисов К.Е.
РУКОВОДИТЕЛЬ ПРОЕКТА
_____________ Шафеева О.П.
ОМСК 1999
Содержание
.I. Введение
II.
Основные соглашения и предположения, использован-ные при создании курсового проектаIII.
Структура объекта.IV.
Вращение объекта вокруг оси Oz.V. Вращение объекта вокруг произвольной оси.
VI.
Вывод изображения объекта на экран.1)
Проецирование.2) Прорисовка грани.
3) Отброс не лицевых граней.
5) Отброс закрытых граней.
6) Закраска граней.
Введение
.Для человека трехмерное пространство является привычной средой обитания, все наши чувства направлены на манипулирование таким пространством. Любая иная среда для человека является инородной и для ориентирования в ней приходится прилагать определенные усилия. Например: если человек будет читать какую-нибудь книгу в течение пяти часов подряд, то он наверняка испытает чувство определенного дискомфорта как физического, так и психологического, но тот же человек свободно может перерабатывать огромные массивы разнородной информации (визуальные образы, звуки, тактильные ощущения), поддерживая разговор с несколькими собеседниками и выполняя сложную работу.
Компьютер долгое время не мог реализовать даже подобия обычного пространства, что порождало серьезные проблемы для многих пользователей. Но развитие компьютерных систем, аппаратного и программного обеспечения позволяют разработчикам использовать все более сложные алгоритмы и приемы.
Конкурентная борьба порождает ориентацию на среднего пользователя, все большее внимание уделяется психологическим аспектам использование компьютерной техники. Современный подход программам утверждает приоритет внешней, интерфейсной части над внутренней, алгоритмической. Сегодня очень большое внимание уделяется проблемам создания трехмерных моделей различных объектов, использования систем виртуальной реальности, создания интуитивного интерфейса пользовательских программ.
Этот курсовой проект предназначен для демонстрации основных принципов создания систем трехмерного моделирования. Для примера выбрана наиболее часто встречающаяся задача: продемонстрировать на экране вращающееся вокруг произвольной оси тело. При создании проекта учтена возможность использования отдельных его частей в других программах. Этот проект должен не только демонстрировать возможности трехмерной графики, но и служить основой для других программ, более сложных и совершенных.
Основные соглашения и предположения, использованные при создании курсового проекта.
Предполагается, что для любой объект с достаточной точностью можно представить многогранником с конечным числом треугольных граней одного цвета. Предполагается, что использующий этот проект имеет определенные познания в программировании на языке
C, знает основы работы видеоадаптера и знаком с линейной алгеброй и аналитической геометрией на плоскости и в пространстве. В дальнейшем будут использоваться некоторые формулы, доказательство которых можно найти в любом учебнике по математике для ВУЗов.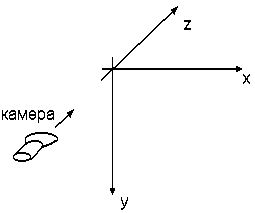
При отображении объектов выбирается следующее расположение координатных осей.
Каждая точка представлена трехмерным радиус-вектором из начала координат в данную точку. Для задания грани задаются номера трех точек, являющихся ее вершинами.
При расчете освещенности каждой грани предполагается, что объект освещается однородным потоком света, направление которого совпадает с направлением камеры (по вектору (0, 0, 1)) , грань не отражает свет, а лишь рассеивает его равномерно по всем направлениям, освещенность в пределах грани не меняется.
Структура объекта.
Модели тел для программы находятся в файлах
*.OB, который содержат список чисел в формате FLOAT (Четырехбайтное число с плавающей десятичной точкой). В процессе работы эти числа записываются в память и интерпретируются следующим образом.|
Смещение от начала |
Значение числа |
Длина |
|
0 |
Число вершин объекта |
4 байта |
|
1, 2, 3 |
X, Y и Z координаты первой вершины |
12 байтов |
|
4, 5, 6 |
X, Y и Z координаты второй вершины |
12 байтов |
|
------------------------ |
------------------------------------------------ |
------------------- |
|
(Число вершин)*3+1 |
Количество граней объекта |
4 байта |
|
(Число вершин)*3 |
Номера вершин грани в списке вершин |
12 байтов |
|
------------------------ |
------------------------------------------------ |
------------------- |
При указании номеров вершин каждой грани необходимо учитывать, что для верного отображения объекта порядок следования вершин должен быть таким, чтобы, находясь вне объекта, мы видели эти вершины следующими против часовой стрелки. Это делается для ускорения работы путем отсечения невидимых граней, о котором будет сказано чуть позднее.
Замечание: При создании объекта нужно найти золотую середину между правдоподобием объекта и количеством граней.
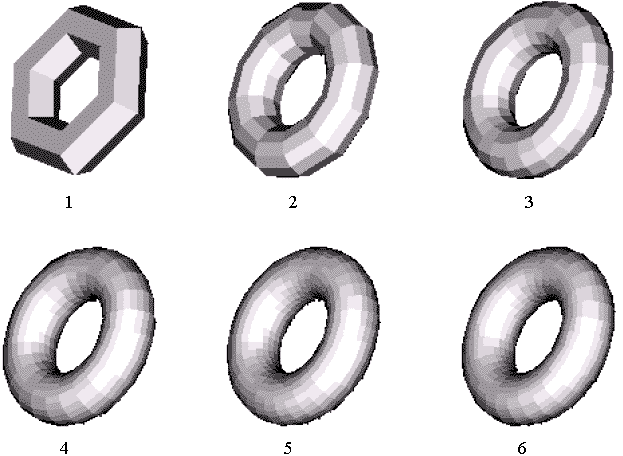
Здесь представлен ряд последовательных аппроксимаций тора. Размер первого объекта 1304 байта, шестого 32408 байт, максимальная скорость вращения первого объекта в 3,2 раза больше, чем шестого. Причем форма объекта очевидна уже со второй модели. К тому же
MS-DOS накладывает ограничение на размер выделяемого участка памяти, поэтому файл не должен быть больше 64 килобайт.
Вращение объекта вокруг оси
Oz.Пусть повернуть некоторую точку с координатами
(x, y, z) на угол j вокруг оси Oz. Если столбец X0 - это столбец координат точки, то после поворота новые координаты образуют некий столбец X. Поворот вокруг оси является линейным преобразованием пространства и может быть представлен в матричной форме, как X=AX0, где A - матрица линейного преобразования. Ее столбцы представляют собой координаты векторов нового базиса в старом базисе.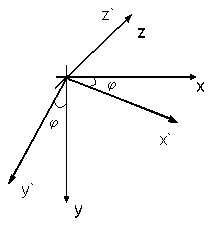
![]()
Из рисунка видно, что
A
=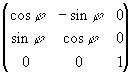 .
.
Находя произведение этой матрицы на столбец координат каждой из вершин, мы получим объект, повернутый на угол j . Если брать малый угол j и последовательно поворачивать объект, то мы получим плавное вращение вокруг оси
Oz.Вращение объекта вокруг произвольной оси.
Вращение объекта вокруг произвольной оси можно рассматривать как вращение вокруг оси
Oz` некоторой системы координат. Матрица такого линейного преобразования находится по формуле A’=CTAC, где C - матрица перехода к новому базису, столбцы которой есть координаты нового базиса в старом.Рассмотрим процесс отыскания матрицы
C. Пусть есть вектор L - направляющий вектор оси вращения, а вектора X=(x1, y1, z1), Y(x2, y2, z2), Z(x3, y3, z3) - координаты базисных векторов нового базиса в старом. Возьмем Z равным L и найдем вектор Y из условия ортогональности Z и Y (т.е. из равенства нуль скалярного произведения (Z,Y)). Т.к. нам важно лишь направление вектора Y, то две его координаты можно приравнять 1.(Z,Y)=0
x3*x1+y3*y1+z3*z1=0
x3+y3+z3*z1=0
z1=-(x3+y3)/z3
Т.о.
Y=(1, 1, -(x3+y3)/z3).В частном случае координата
z3 может быть равна нулю, тогда нужно взять z1=0, и находить уже координаты x1 и y1.Вот фрагмент программы, производящий данные вычисления. Указатели
*X, *Y, *Z указывают на координаты этих векторов.if(*(Z+2)==0) /* Первая координата нулевая? */
{
if(*(Z)==0) /* А вторая? */
{
*(Y+2)=0;
*(Y+1)=0;
*(Y)=1;
}
else
{
*(Y+2)=0;
*(Y+1)=1;
*(Y+0)=-*(Z+1)/(*Z);
}
}
else
{
*(Y+0)=1;
*(Y+1)=1;
*(Y+2)=-1*(*Z+*(Z+1))/(*(Z+2));
}
После этого легко можно найти вектор
X как векторное произведение [Z,Y]. Вот текст функции, которая делает это.void mltp( float *Y, float *Z, float *X)
{
*(X+0)=*(Y+1)*(*(Z+2))-(*(Y+2))*(*(Z+1));
*(X+1)=*(Y+2)*(*(Z+0))-(*(Y+0))*(*(Z+2));
*(X+2)=*(Y+0)*(*(Z+1))-(*(Y+1))*(*(Z+0));
}
Нам необходимо получить ортонормированный базис, поэтому нужно разделить координаты векторов
X, Y, Z на их длину.Теперь составим матрицу
C и посчитаем матрицу A’.Вывод изображения объекта на экран.
1) Проецирование.
Т.к. перспектива не учитывается, то на экран нужно выводить обычную ортогональную проекцию объекта. Двумерные координаты проекции точки получаются отбрасыванием третьей координаты.
2) Прорисовка грани.
Проекция грани представляет собой закрашенный треугольник. Целесообразно написать собственный алгоритм рисования такого треугольника, не использую медленные стандартные функции.
Изображение треугольника на экране можно представить как набор горизонтальных отрезков, причем из-за того, что треугольник - фигура выпуклая, каждой строке экрана соответствует не более одного отрезка. Поэтому достаточно пройтись по всем строкам экрана, с которыми пересекается треугольник (то есть, от минимального до максимального значения y для вершин треугольника), и нарисовать соответствующие горизонтальные отрезки.
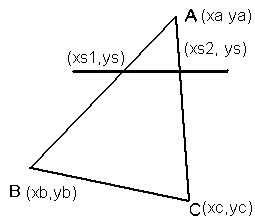
Отсортируем вершины так, чтобы вершины A, B, C шли по убыванию ординаты. Теперь введем переменную ys и будем изменять ее от ya до yc, находя абсциссы точек пересечения прямой y=ys со сторонами треугольника и проводя отрезки с концами в точках (xs1, ys) и (xs2, ys). При этом нужно учитывать, что если ys>yb, то прямая пересекает отрезки AB и AC, а если ys<yb, то - BC и AC.
Для нахождения точек пересечения можно воспользоваться уравнением прямой, проходящей через две точки. Например
, для пересечения с отрезком AB можно записать:![]()
Отсюда,
xs1=xa+(xb-xa)(ys-ya)/(yb-ya).Необходимо следить за случаями, когда
ya=yb или ya=yc.3) Отброс не лицевых граней.
Т.к. тело замкнуто, то для каждой грани мы можем увидеть только одну ее сторону - лицевую. Перед прорисовкой грани нужно проверить, обращена грань к нам лицевой или изнаночной стороной. Для этого создается массив внешних нормалей к граням. Т.к. вершины изначально упорядочены так, что
, находясь вне объекта, мы видим эти вершины следующими против часовой стрелке, то нормаль можно считать как векторное произведение вектора от первой до второй вершины и вектора от первой до третьей вершины.Вот как это делается в программе:
a[0]=x2-x1;
a[1]=y2-y1;
a[2]=z2-z1;
b[0]=x3-x1;
b[1]=y3-y1;
b[2]=z3-z1;
n_f[0]=a[1]*b[2]-a[2]*b[1];
n_f[1]=-a[0]*b[2]+a[2]*b[0];
n_f[2]=a[0]*b[1]-a[1]*b[0];
Здесь
x1, x2, x3, y1, y2, y3, z1, z2, z3 - координаты соответствующих вершин, а n_f[] - вектор нормали.Удобнее пользоваться ортом вектора нормали. Для его получения нужно вектор нормали разделить на его длину.
5) Отброс закрытых граней.
К сожалению, метод отсечения не лицевых граней, замечательно работающий для выпуклых тел, не может полностью решить проблемы отсечения невидимых граней. Вот пример этого:


Некорректное Верное изображение
изображение
Для корректировки изображения используют алгоритм художника. Грани сортируются по убыванию значения средней аппликаты всех ее вершин. Для сортировки в данном курсовом проекте был использован алгоритм “быстрой сортировки”.
Далее приведен пример функции, проводящей сортировку граней. В этом примере *а – указатель на начало массива средних значений удаленности граней, ilo и ihi – смещение первой и последней граней для сортировки. *iz – указатель на массив номеров граней в том порядке, в котором они будут прорисовываться (в начале заполнен числами от ilo до ihi по-порядку).
void qsrt (int *a, int ilo, int ihi )
{
int t;
int lo, hi, mid;
lo=ilo;
hi=ihi;
mid=*(a+(hi+lo)/2);
do
{
while(*(a+lo)>mid) lo++;
while(*(a+hi)<mid) hi--;
if(lo<hi || lo==hi)
{
t=*(a+lo); /* Меняем элементы */
*(a+lo)=*(a+hi);
*(a+hi)=t;
t=*(iz+lo); /* Меняем индексы */
*(iz+lo)=*(iz+hi);
*(iz+hi)=t;
lo++;
hi--;
}
}
while((lo<hi) || (lo==hi));
if(hi>ilo) qsrt(a, ilo, hi);
if(lo<ihi) qsrt(a, lo, ihi);
}
Есть случаи, когда такая оценка видимости не даст нам правильного ответа, но если при создании объекта за этим следить, то алгоритм художника и отсечение не лицевых граней дадут неплохой результат.
6) Закраска граней.
Грани раскрашиваются в различные оттенки серого в зависимости от угла между гранью и направлением светового потока. Для начала вся цветовая палитра заполняется так, чтобы с возрастанием номера цвета росла его яркость. Для ускорения работы программы использует непосредственное программирование портов видеоадаптера.
Эта функция выглядит так
void set_col(char col, char r, char g, char b)
{
outportb(0x3c8,col);
outportb(0x3c9,r);
outportb(0x3c9,g);
outportb(0x3c9,b);
}
void grayscale(void)
{
unsigned long int i;
for(i=0;i<256;i++)
{
set_col (i, i/4, i/4, i/4);
}
}
Для нахождения косинуса между нормалью грани
N=(n1, n2, n3) и направлением светового потока Z=(0, 0, 1) нужно найти их скалярное произведение (длины этих векторов равны 1).(N, Z)=n1*0+n2*0+n3*1=n3
Т.о. рисуются только те грани, у которых аппликата вектора нормали
n3<0 (лицевые грани), причем цвет грани col=n3*255.